データ分析において、変数間の関係性を理解することは非常に重要です。しかし、常に変数間に単純な線形関係があるとは限りません。そのような場合、多項式回帰が役立ちます。この記事では、多項式回帰の概要と、Pythonを使った実装方法について説明します。
多項式回帰とは
多項式回帰は、説明変数と目的変数の間に非線形の関係があると仮定し、その関係を多項式を用いてモデル化する手法です。単純な線形回帰では、以下のような1次式でモデル化します。
$$y = b0 + b1 * x$$
一方、多項式回帰では、次数を上げた項を追加することで、曲線的な関係性を表現できます。例えば、2次の多項式回帰は以下のようになります。
$$y = b0 + b1 * x + b2 * x^2$$
多項式回帰の実装 (Pythonの場合)
Pythonでscikit-learnを使えば、多項式回帰を簡単に実装できます。以下にサンプルコードを示します。
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
# データの準備 (ここでは省略)
X, y = ...
# モデルの構築
model = Pipeline([
('poly', PolynomialFeatures(degree=2)), # 2次の多項式を作成
('linear', LinearRegression()) # 線形回帰モデルを適用
])
# モデルの学習
model.fit(X, y)
# 予測
y_pred = model.predict(X)ここでは、PolynomialFeaturesを使って多項式特徴量を作成し、それをLinearRegressionに渡すことで多項式回帰を実現しています。degreeパラメータで多項式の次数を指定できます。
注意点
多項式回帰は強力な手法ですが、次の点に注意が必要です。
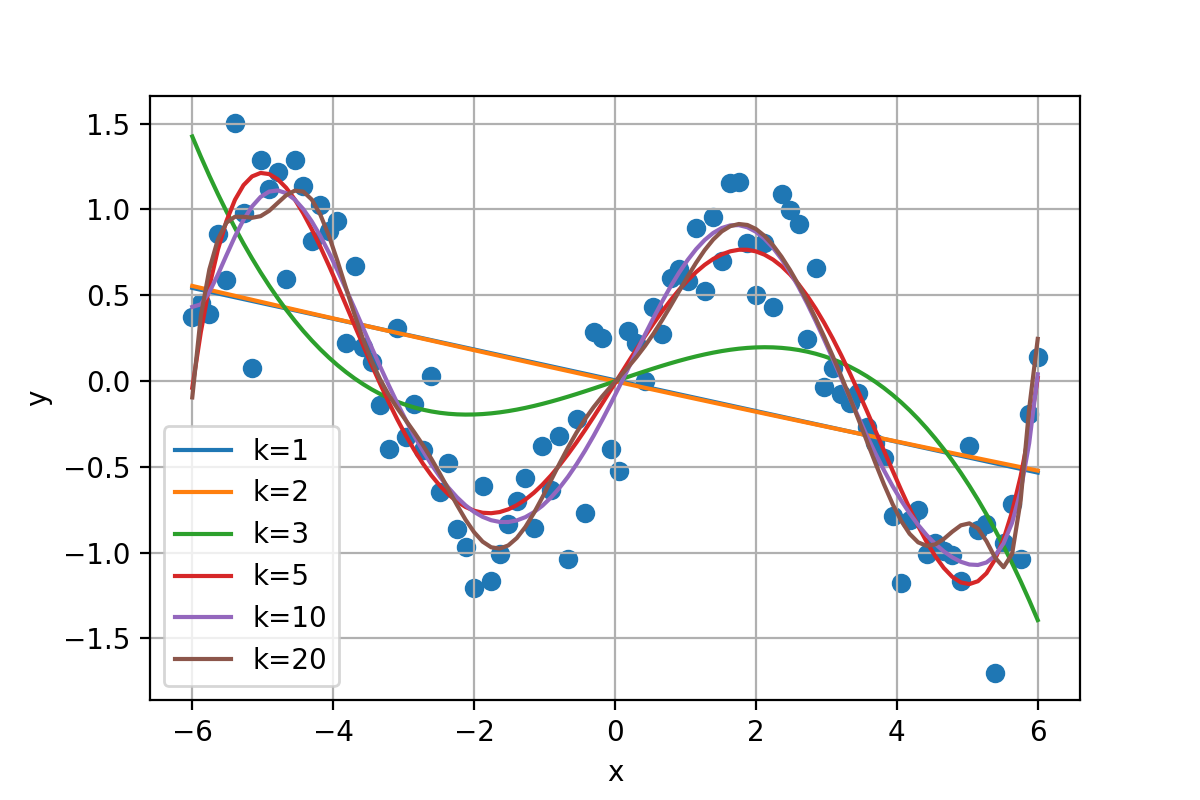
- 次数を上げすぎると過学習を引き起こす可能性がある
- 外挿 (学習データの範囲外への予測) には適していない
- 特徴量の尺度が大きく異なる場合は、標準化が必要
適切に使えば、多項式回帰は非線形な関係性のモデル化に役立ちます。データの特性を見極め、慎重にモデルを選択することが大切です。
以上が、多項式回帰の概要とPythonでの実装方法です。非線形な関係性の理解に、ぜひ多項式回帰を活用してみてください。