適応領域の設定
気象予測を量子機械学習をつかって解きます。
具体的には、大阪市の天気予測をします。
データの入手・確認
気象庁から大阪市の直近一ヶ月分のCSVデータをダウンロードします。(2022/9/27日時点)
ダウンロードしたCSVは以下です。(2022年8月30日 ~ 2022年9月30日)
天気に関係のある項目を抽出しました。
ダウンロードした時刻:2022/10/01 14:38:59
,大阪,大阪,大阪,大阪,大阪
,平均現地気圧(hPa),合計全天日射量(MJ/㎡),平均雲量(10分比),降水量の合計(mm),天気概況(昼:06時~18時)
2022年8月30日,1002.8,13.01,10.0,6.5,曇一時雨
2022年8月31日,998.8,23.13,6.3,0.0,晴時々薄曇
2022年9月1日,1001.1,8.88,10.0,20.5,曇時々雨
2022年9月2日,1004.8,20.43,8.5,21.5,晴時々曇一時雨、雷を伴う
2022年9月3日,1005.0,15.35,9.3,17.5,晴後曇一時雨
2022年9月4日,1004.6,19.90,3.5,0.0,晴後一時曇
2022年9月5日,1002.9,19.27,3.3,0.0,晴一時曇
2022年9月6日,998.4,14.47,9.5,1.0,晴後曇一時雨
2022年9月7日,1003.6,17.47,9.8,2.5,曇一時晴
2022年9月8日,1004.8,7.79,10.0,39.0,曇後一時雨
2022年9月9日,1004.6,9.35,10.0,5.0,曇時々雨
2022年9月10日,1005.1,19.87,7.5,0.5,晴時々曇
2022年9月11日,1004.2,22.28,2.8,--,晴
2022年9月12日,1003.4,21.10,5.0,--,晴一時薄曇
2022年9月13日,1004.3,21.74,6.8,--,薄曇後晴
2022年9月14日,1004.5,19.19,7.0,--,薄曇時々晴
2022年9月15日,1003.0,19.31,7.0,--,薄曇後晴
2022年9月16日,1002.1,22.04,7.3,--,晴後薄曇
2022年9月17日,1000.4,8.23,10.0,3.5,曇
2022年9月18日,994.8,11.89,10.0,--,曇
2022年9月19日,984.1,7.09,9.8,16.0,曇一時雨
2022年9月20日,995.8,12.89,9.8,16.0,曇
2022年9月21日,1004.9,13.43,9.3,0.0,曇時々晴
2022年9月22日,1005.5,15.15,10.0,2.0,曇一時雨
2022年9月23日,1000.9,2.62,9.8,17.0,雨後曇
2022年9月24日,1002.8,19.63,5.3,--,晴
2022年9月25日,1005.6,21.19,2.3,--,晴
2022年9月26日,1005.8,20.74,1.0,--,晴
2022年9月27日,1003.7,10.36,9.5,18.5,曇後雨
2022年9月28日,1001.3,12.33,10.0,0.0,曇
2022年9月29日,1003.4,11.88,9.5,0.0,曇一時晴後一時雨
2022年9月30日,1005.4,19.61,0.5,--,晴※APIで取得するなら
気象データの入手は
Intertrustから
Pythonのライブラリrequestsを使ってもできるみたいです。
Intertrustは世界各地の気象データが集積されています。
APIも提供されています。
14日無料トライアルの期間ではデータの取得が可能です。
実装
インポート
from blueqat import Circuit
from blueqat.pauli import Z
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as pltデータ加工
# 気象データ(2022年08月26日 ~ 2022年09月26日)
data = np.array(
[
[1002.8,13.01,10.0,6.5],
[998.8,23.13,6.3,0.0],
[1001.1,8.88,10.0,20.5],
[1004.8,20.43,8.5,21.5],
[1005.0,15.35,9.3,17.5],
[1004.6,19.90,3.5,0.0],
[1002.9,19.27,3.3,0.0],
[998.4,14.47,9.5,1.0],
[1003.6,17.47,9.8,2.5],
[1004.8,7.79,10.0,39.0],
[1004.6,9.35,10.0,5.0],
[1005.1,19.87,7.5,0.5],
[1004.2,22.28,2.8,0.0],
[1003.4,21.10,5.0,0.0],
[1004.3,21.74,6.8,0.0],
[1004.5,19.19,7.0,0.0],
[1003.0,19.31,7.0,0.0],
[1002.1,22.04,7.3,0.0],
[1000.4,8.23,10.0,3.5],
[994.8,11.89,10.0,0.0],
[984.1,7.09,9.8,16.0],
[995.8,12.89,9.8,16.0],
[1004.9,13.43,9.3,0.0],
[1005.5,15.15,10.0,2.0],
[1000.9,2.62,9.8,17.0],
[1002.8,19.63,5.3,0.0],
[1005.6,21.19,2.3,0.0],
[1005.8,20.74,1.0,0.0],
[1003.7,10.36,9.5,18.5],
[1001.3,12.33,10.0,0.0],
[1003.4,11.88,9.5,0.0],
[1005.4,19.61,0.5,0.0],
]
)
df = pd.DataFrame(data, columns=['hPa','MJ','cloud','precipitation']) # 平均現地気圧(hPa),合計全天日射量(MJ/㎡),平均雲量(10分比),降水量の合計(mm)
# 雲量で天気を判断
y = df["cloud"]
X = df.drop(columns=["cloud"], axis=1)
X_train, X_val, y_train, y_val = train_test_split(
X,
y,
test_size=0.2,
random_state=1
)モデル開発
3量子ビットでやります。
N = 3シードを1に、パラメーターは18個用意します。
np.random.seed = 1
params = [np.random.rand() for _ in range(N*6)] # param*18ハミルトニアン
hamiltonian = 1*Z[0]*Z[1]*Z[2]微分用の誤差と学習率。
h = 1e-6
e = 0.1arr_loss = []
for k in range(100):
for item, answer in zip(X_train.values, y_train.values):
circuit = Circuit()
print(item)
for i in range(N):
circuit.rx(params[i*3+0])[i].ry(params[i*3+1])[i].rz(params[i*3+2])[i]
circuit.cz[0,1].cz[1,2].cz[2,3].cz[3,0]
for i in range(N):
circuit.rx(np.pi*2*item[i]/100)[i]
for i in range(N):
circuit.rx(params[i*3+N*3])[i].ry(params[i*3+N*3+1])[i].rz(params[i*3+N*3+2])[i]
expt = circuit.run(hamiltonian = hamiltonian)
loss = (expt - answer/100)**2
grad_temp = np.zeros(N*6)
for j in range(N*6):
params_temp = params[:]
angle_temp = params_temp[j]
params_temp[j] += h
circuit = Circuit()
for i in range(N):
circuit.rx(params_temp[i*3+0])[i].ry(params_temp[i*3+1])[i].rz(params_temp[i*3+2])[i]
circuit.cz[0,1].cz[1,2].cz[2,3].cz[3,0]
for i in range(N):
circuit.rx(np.pi*2*item[i]/100)[i]
for i in range(N):
circuit.rx(params_temp[i*3+N*3])[i].ry(params_temp[i*3+N*3+1])[i].rz(params_temp[i*3+N*3+2])[i]
expt_temp = circuit.run(hamiltonian = hamiltonian)
loss_temp = (expt_temp - answer/100)**2
grad_temp[j] = (loss_temp - loss)/h
params -= grad_temp*e
arr_loss.append(loss)
print(loss)評価/予測
plt.plot(arr_loss)
plt.show()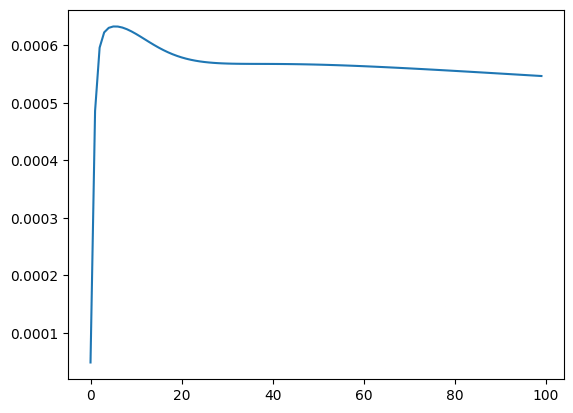
適当な日の天気を予測してみます。
# 2003年8月18日のデータ。雲量は8.8で一応晴れ。
X_test = [1004.8,18.6,0.5]
circuit = Circuit()
for i in range(N):
circuit.rx(params[i*3+0])[i].ry(params[i*3+1])[i].rz(params[i*3+2])[i]
circuit.cz[0,1].cz[1,2].cz[2,3].cz[3,0]
for i in range(N):
circuit.rx(np.pi*2*X_test[i]/100)[i]
for i in range(N):
circuit.rx(params[i*3+N*3])[i].ry(params[i*3+N*3+1])[i].rz(params[i*3+N*3+2])[i]
expt = circuit.run(hamiltonian = hamiltonian)
print(expt*100)6.25270091561785とでました。
雲の量が1割以下(0~1割)の状態を「快晴」、
2割から8割の状態を「晴れ」、
9割以上の状態を「曇り」といいます。一応、2003年8月18日は晴れ、予測結果も晴れということで良いのではないでしょうか。
結論
入力値が安牌すぎて使いものにならない。
画像(QCNN)か、GSWRシステムとQMLのハイブリッドか(よくわかってない)を調べないといけない。
